Osg坐标系与四元数
1. osg 坐标系统
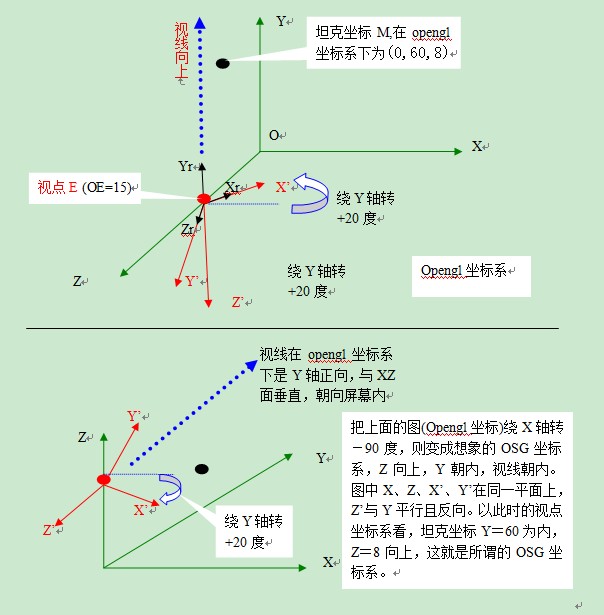
opengl坐标系: X向右,Y向上,Z向外
OSG坐标系统:X向右,Y向里,Z向上
无论是OpenGL,DirectX还是OSG,一般都会遵守SRT(Scale/Rotate/Translate)的运算顺序来完成符合矩阵的构建,其公式为:
M =Ms * Mr * Mt
2. 四元数
基础知识
前面说过,一个四元数可以表示为q = w + xi + yj + zk。
为了方便,我们下面使用q = ((x, y, z),w) = (v, w),其中v是向量,w是实数,这样的式子来表示一个四元数。
我们先来看问题的答案。我们可以使用一个四元数q=((x,y,z)sinθ2, cosθ2) 来执行一个旋转。具体来说,如果我们想要把空间的一个点P绕着单位向量轴u = (x, y, z)表示的旋转轴旋转θ角度,我们首先把点P扩展到四元数空间,即四元数p = (P, 0)。那么,旋转后新的点对应的四元数(当然这个计算而得的四元数的实部为0,虚部系数就是新的坐标)为:
p′=qpq−1
其中,q=(cosθ2, (x,y,z)sinθ2) ,q−1=q∗N(q),由于u是单位向量,因此 N(q)=1,即q−1=q∗。右边表达式包含了四元数乘法。相关的定义如下: 四元数乘法:q1q2=(v1→×v2→+w1v2→+w2v1→,w1w2−v1→⋅v2→)
共轭四元数:q∗=(−v⃗ ,w)
四元数的模:N(q) = √(x^2 + y^2 + z^2 +w^2),即四元数到原点的距离
四元数的逆:q−1=q∗N(q)
它的证明这里不再赘述,有兴趣的可以参见这篇文章。主要思想是构建了一个辅助向量k,它是将p绕旋转轴旋转θ/2得到的。证明过程尝试证明wk∗=kv∗,以此证明w与v、k在同一平面内,且与v夹角为θ。
我们举个最简单的例子:把点P(1, 0, 1)绕旋转轴u = (0, 1, 0)旋转90°,求旋转后的顶点坐标。首先将P扩充到四元数,即p = (P, 0)。而q = (u*sin45°, cos45°)。求p′=qpq−1的值。建议大家一定要在纸上计算一边,这样才能加深印象,连笔都懒得动的人还是不要往下看了。最后的结果p` = ((1, 0, -1), 0),即旋转后的顶点位置是(1, 0, -1)。
如果想要得到复合旋转,只需类似复合矩阵那样左乘新的四元数,再进行运算即可。
我们来总结下四元数旋转的几个需要注意的地方:
用于旋转的四元数,每个分量的范围都在(-1,1);
每一次旋转实际上需要两个四元数的参与,即q和q*;
所有用于旋转的四元数都是单位四元数,即它们的模是1;
下面是几点建议:
实际上,在Unity里即便你不知道上述公式和变换也丝毫不妨碍我们使用四元数,但是有一点要提醒你,除非你对四元数非常了解,那么不要直接对它们进行赋值。
如果你不想知道原理,只想在Unity里找到对应的函数来进行四元数变换,那么你可以使用这两个函数:Quaternion.Euler和Quaternion.eulerAngles。它们基本可以满足绝大多数的四元数旋转变换。
参考:
